The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones. It starts with 0 and 1 and continues as follows:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …
This sequence was introduced to Western mathematics by Leonardo of Pisa, also known as Fibonacci, in his 1202 book Liber Abaci. However, it was first described in Indian mathematics as early as 200 BC in connection with Sanskrit poetry.
Applications of Fibonacci Numbers
Fibonacci numbers appear in various fields, including
- Mathematics—Used in algorithms, data structures, and number theory.
- Fibonacci numbers can be found in Pascal’s Triangle. The sums of the diagonals in Pascal’s Triangle are Fibonacci numbers.
- In number theory, Fibonacci numbers have unique properties. For example, every nth Fibonacci number is the sum of the previous n Fibonacci numbers.
- The Fibonacci sequence is used in computer algorithms, particularly in recursive algorithms and data structures like Fibonacci heaps.
- Biology—Found in the branching of trees, arrangement of leaves, and the spirals of pinecones and sunflowers.
- Art & Architecture—Closely related to the Golden Ratio, which is often used in design and aesthetics.
- Leonardo da Vinci used the Golden Ratio in his famous painting, “The Last Supper.” The dimensions of the table and the positioning of the apostles follow this ratio.
- The Fibonacci sequence is used in modern art, too. Artists like Salvador Dalí incorporated these numbers into their works to achieve balance and harmony.
- The Great Pyramid of Giza is believed to have proportions that approximate the Golden Ratio, linking it to Fibonacci numbers.
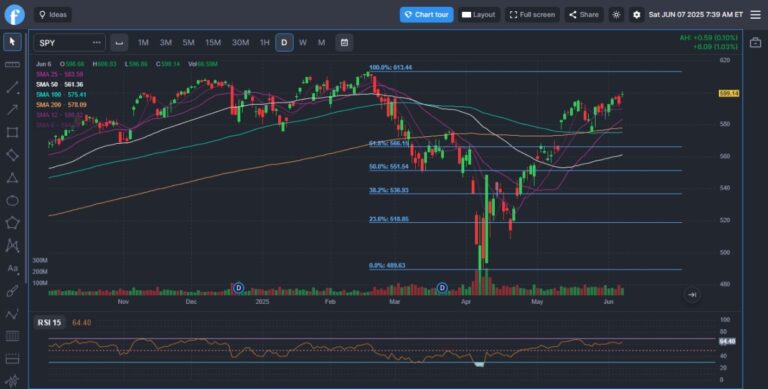
- Finance—Applied in technical analysis, particularly in Elliott Wave Theory. The Fibonacci Ratios are widely used in trading strategies.